Strong Nonconsequentialist Solution to the New Problem of Numbers in Morality

Jackson Anderson

The popularity of thought experiments in philosophy is probably rooted in their ability to focus a topic so that possible solutions may be more directly explored and critiqued. As cases evolve and variations arise, new problems may reveal themselves and challenge once-satisfactory solutions. In her article, “The New Problem of Numbers in Morality”, Fiona Woollard (2014) does exactly this by arguing against the ability of popular Nonconsequentialist solutions to the Old Problem of Numbers in Morality to satisfy her New Problem of Numbers in Morality. In this paper, I will both explain and argue against Woollard’s subsequent conclusion, that one cannot simultaneously adhere to the Individualistic Restriction whilst also claiming that numbers matter in the trolley cases.

In order to explain Woollard’s argument regarding the New Problem of Numbers, I must first describe the Old Problem of Numbers. The Old Problem stems from the “Rocks” whom-to-rescue case, which Woollard (2014) describes as follows (p. 631):

Rocks: Five people are stranded on one rock. One person is stranded on another. In your boat, you are able to reach either rock before the tide comes in, but not both. Anyone left standing on a rock at high tide will drown (Anscombe, 1977, p. 17).

Woollard then describes the spectrum of possible responses, with the intuitive answer to save the greater number on one end and Taurek’s staunchly individualist argument that “when all else is equal, we must toss a coin, giving each person an equal chance to be saved” on the other (p. 632).

It is important to note that all but Taurek’s response grant the difference in numbers a role in the decision. As Woollard explains, this is a problem for Nonconsequentialists who abide by the Individualistic Restriction[1] which bars the “appeal to the aggregated good of distinct individuals” (p. 632). These “Strong” Nonconsequentialists, as Woollard calls them (p. 632), face the Old Problem of being stuck between “abandoning their position [of individualism] and accepting highly counter-intuitive claims” (p. 633).

While there have been numerous Strong Nonconsequentialist attempts to solve the Old Problem of Numbers, Woollard argues that even the most popular variations[2] become inadequate when translated to numbers cases that involve killing. To arrive at this conclusion, which she names the New Problem of Numbers, Woollard tests Strong Nonconsequentialist reasoning against variations of Judith Jarvis Thomson’s Trolley Case. As such, it is best to begin by examining Thomson’s Trolley Case (below):

Thomson’s Trolley: Five people are trapped on the track ahead of a runaway trolley. You can turn the trolley onto a side-track where a single person is trapped. If you do nothing, the one will live and the five will die. If you turn the trolley, the five will live and the one will die (Thomson, 1976, p. 207).

Parallels to the Rocks case are immediately evident, with the decision being between the fate of a group of 5 and a single individual. Once again, the intuitive response seems to be to save the greater number. What differentiates Thomson’s Trolley from Rocks, however, is the way in which the individuals of either group die; Those on the main track are simply allowed to die while the individual on the side track is killed by the third party who switches the tracks. If this distinction does not at first seem material, consider Woollard’s variation of the Trolley Case:

Woollard’s Trolley: A single person is trapped on the track ahead of a runaway trolley. You can turn the trolley onto a side-track where a different, single person is trapped. If you do nothing, the individual on the side track will live and the individual on the main track will die. If you turn the trolley, the individual on the main track will live and the individual on the side track will die (Woollard, 2014, p. 633)

With the numbers equalized, the intuitive response now appears to be to allow the individual on the main track to die rather than kill the individual on the side track. As Woollard states, “It seems obviously impermissible to turn the trolley towards one simply to save a single innocent stranger” (p. 633). This distinction – that, all things equal, it is worse to do harm than to allow harm to occur – is popularly known as the Doctrine of Doing and Allowing (DDA). Woollard’s analysis highlights the fact that while the commonsense answer to Woollard’s Trolley adheres to the DDA, the commonsense answer to Thomson’s Trolley seems to, by itself, violate the DDA. With the only difference between these cases being the numbers, Woollard rationalizes that the numbers must also matter. That is, the only way to preserve both intuitive responses is to admit that the numbers should also be considered. Below is a summary of this reasoning:

1. The intuitive answer to Thomson’s Trolley is to save the 5 (Greater Number)

2. The intuitive answer to Woollard’s Trolley is to allow the one to die (DDA)

3. The only difference between the two cases is the numbers

4. Thus, either our intuition is wrong or the numbers do matter

With this reasoning established, Woollard then frames the New Problem of Numbers for Strong Nonconsequentialists. To do this, Woollard both defends the intuitive response to Thomson Trolley and argues that the numbers cannot matter to a Strong Nonconsequentialist. First, Woollard defends the intuitive responses to Thomson Trolley. The Strong Nonconsequentialist does not contradict the Individualistic Restriction by arriving at the intuitive conclusion to Woollard Trolley (DDA). However, the Strong Nonconsequentialist would then have to hold that the DDA is so powerful a constraint that it outweighs the intuitive response to Thomson Trolley. That is, that killing is so wrong that, unfortunate as it is, it is right to allow the five to perish in place of the one. The incredibly counter-intuitive nature of this conclusion is revealed through Woollard’s examination of the Extreme Trolley case (my interpretation below):

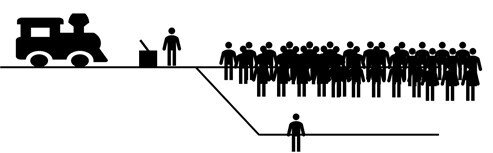
Extreme Trolley: 5,000,000 people are trapped on the track ahead of a runaway trolley. You can turn the trolley onto a side-track where a single person is trapped. If you do nothing, the one will live and the 5,000,000 will die. If you turn the trolley, the 5,000,000 will live and the one will die.

The Strong Nonconsequentialist, in order to stay consistent, would need to hold that the 5,000,000 individuals should be allowed to die rather than killing the one. The extreme implications of this possible Strong Nonconsequentialist conclusion seems, at the very least, bizarre.[3]

To avoid this bizarre outcome, the Strong Nonconsequentialist would need to deny the opposing viewpoint, that the numbers do matter. As such, Woollard then addresses the implications of this intuition-confirming response. Woollard explains that Strong Nonconsequentialists cannot accept this conclusion without also violating the Individualistic Restriction; “…admitting that what we are required to do can depend on costs and benefits aggregated over distinct individuals…” (p. 640). This is a serious concern, as the Individualistic Restriction is the central component of Strong Nonconsequentialism.

This logic certainly seems to leave the Strong Nonconsequentialist with the burden of proof. This is furthered by Woollard’s objections to two popular Strong Nonconsequentialist solutions to the Old Problem of Numbers (F. M. Kamm’s Balancing/Tiebreaker Argument (1985) and Véronique Munoz-Dardé’s Non-Comprehensive Reasons Argument (2005)). By demonstrating how these attempts appear to fall flat in the face of her now-established New Problem of Numbers (which is the subject of her article “The New Problem of Numbers in Morality” (2014)), Woollard concludes that one “must either abandon her Nonconsequentialism” by accepting that individual reasons may be aggregated, or “claim that numbers do not matter in the Trolley… [which lead to] highly-counterintuitive results” (p. 640).

Below is my summation of Woollard’s argument for the New Problem of Numbers and her corresponding conclusion regarding Strong Nonconsequentialism:

1. The intuitive answer to Thomson’s Trolley is to save the 5 (Greater Number).

2. The intuitive answer to Woollard’s Trolley is to allow the one to die (DDA).

3. The only difference between the two cases is the numbers.

4. Thus, either our intuition is wrong or the numbers do matter.

   a. If our intuition is wrong, then we would have to accept the extreme implications of Extreme Trolley or reject the DDA. By definition, affirmations of this response would be counter-intuitive.

   b. If the numbers matter, then we would have to reject the Individualistic Restriction by aggregating distinct individuals.

5. The Strong Nonconsequentialist must either accept extremely counter-intuitive implications of Extreme Trolley, OR reject the Individualistic Restriction (and, thus, Strong Nonconsequentialism).

6. Thus, the Strong Nonconsequentialist cannot both accept intuitive answers to the trolley cases AND accept that the numbers matter.

With Woollard’s stance established, I will now argue for an alternative Strong Nonconsequentialist solution to the New Problem of Numbers. This solution directly contradicts Woollard’s conclusion by providing the Strong Nonconsequentialist with a way to both accept the intuitive answers to the trolley cases and accept that the numbers do matter.

I will begin by considering the Individualistic Restriction (that which makes Strong Nonconsequentialism “Strong”, according to Woollard). As previously stated, this idea limits concern to only the reasons of individuals. While this clearly prohibits the aggregation of distinct individuals when making decisions, it is quite dependent on the accumulation of reasons within each distinct individual. For example, consider a situation where two individuals make up 100% of a lottery pool, each with 50% odds of winning. If, all else equal, the prize for the first individual is two cars and the prize for the second individual is one car (each car equivalent), the first individual would have a greater amount of possible benefit at stake. This concept is what allows, and perhaps requires, the Strong Nonconsequentialist to accept DDA in its simplest form.

With this in mind, reconsider the Woollard Trolley:

Woollard’s Trolley: A single person is trapped on the track ahead of a runaway trolley. You can turn the trolley onto a side-track where a different, single person is trapped. If you do nothing, the individual on the side track will live and the individual on the main track will die. If you turn the trolley, the individual on the main track will live and the individual on the side track will die (Woollard, 2014, p. 633).

The basis of Woollard Trolley, and every other trolley or rescue case considered, is in all things being equal. For all things to be equal, each distinct individual in the situation must be the same and be interchangeable with one another. Their claims must be either identical or corresponding. This is the reason why, in Woollard Trolley, our intuition is most clearly the DDA: The individual on the main track (B) has a claim not to be allowed to die, the individual on the side track (C) has a claim not to be killed, and the individual at the lever (A) does not appear to have a corresponding claim at all (or, at the very least, not a claim that is comparable in importance to those of the other two). As Woollard stated, the commonsense answer appears to be to allow the one to die rather than to kill. What Woollard does not emphasize, however is how unrealistic this case is. Given that all else is equal, the individuals in this situation exemplify a maximum of one concern (either to not die or not be killed). There must, then, be absolutely zero concern for or claim regarding any of the other two individuals in this specific situation. That is, empathetic claims are not incorporated into this case. This makes it clear that in Woollard Trolley the included individuals are probably a poor representation of the people we typically encounter in life. It seems intuitive to assume that the common person has at least some sort of concern for the well-being of others or would at the very least be bothered by their demise.

Consider the following case where I attempt to visualize this concept.

Empathetic Woollard Trolley:

Although most would probably hold, as I do, that the intuitive response is still to follow the DDA, the Empathetic Woollard Trolley helps make clear that our commonsense responses regarding people seem to assume that we are dealing with relatively common people (those who have at least some sort of empathy, or otherwise act in a common fashion). Since commonsense itself is a generalized concept, it is likely impossible to have a perfectly reflective version of Woollard Trolley that would apply in most situations; However, the intuitiveness of at least some sort of empathy assumption indicates that Empathetic Woollard’s Trolley is closer to this ideal trolley than the original Woollard Trolley. So, Woollard Trolley is a very unrealistic case that happens to have the same intuitive answer as most other, more realistic variations (such as the Empathetic Woollard Trolley).

Unrealistic cases (as in, the individuals involved lack realistic, common qualities) create concerning intuitive confusion if their uniqueness is not made clear. This point is highlighted by reexamining Extreme Trolley:

Extreme Trolley: 5,000,000 people are trapped on the track ahead of a runaway trolley. You can turn the trolley onto a side-track where a single person is trapped. If you do nothing, the one will live and the 5,000,000 will die. If you turn the trolley, the 5,000,000 will live and the one will die.

When reconsidering the implications of Extreme Trolley under the lens just used to distinguish Woollard Trolley from Empathetic Woollard Trolley, the bizarreness and simplicity of the concept is made clear very quickly. The odds of a life-or-death situation such as this occurring and including 5,000,002 individuals whose only concerns include their own claim either to not die or not be killed, thus zero concern whatsoever for the other 5,000,001 individuals around them, seem incredibly slim. Integrating empathy seems to do a great deal in making this case more realistic:

Empathetic Extreme Trolley:

It is because of additional psychological claims such as empathy for others (all things being equal) that I argue allows the Strong Nonconsequentialist to escape the extremely counter-intuitive implications of using the DDA alone to make a decision rather than considering the numbers. By marrying the concept of additional psychological claims (I will focus almost exclusively on empathy, for it seems to be the most obvious and helpful) with my previously established claim that the Individualistic Restriction includes the accumulation of reasons within distinct individuals, a Strong Nonconsequentialist account for the numbers can be made. Essentially, the accumulation of additional psychological claims within any one of the individuals on the track with greater numbers will eventually “overtake” the DDA by tipping the intuition in favor of the numbers. I will now provide an extended example to visualize this concept:

For the following, remember that all individuals are equal in thought and action, with corresponding reasons that would be shared by any other included individual if their positions were swapped.

Consider once again the Empathetic Woollard Trolley.

There are DDA equivalent claims (either to not be allowed to die or to not be killed) and empathetic claims (either that another not be allowed to die or to not be killed) for each individual. Note that A’s DDA equivalent claim is irrelevant, as it will be unaffected by either outcome. In order to examine each individual’s accumulated reasons (benefit/harm) that would differ between outcomes, I will give each claim an arbitrary quantitative value relative to those of the other claims. If these individuals are to be considered “common”, then we are probably not mistaken in considering them to be neither excessively egotistic nor excessively altruistic (I will provide specific reasoning for this later).[4] As such, the relative weight of each claim would intuitively fall in the following order (most to least):

1. Claim to not be killed

2. Claim to not be allowed to die

3. Claim that another is not killed

4. Claim that another is not allowed to die

The DDA explains the ranking of 1 and 2 relative to each other, as well as that between 3 and 4. The supremacy of 1 & 2 over 3 & 4 reflects what seems to be the intuitive claim that the common person is probably marginally more egotistic than altruistic when regarding strangers. Even if this is false, and the average individual is either perfectly neutral or marginally altruistic, the overall concept is not contradicted (more on this later). Now, I will arbitrarily assign quantitative values to each relative to their rankings so that accumulated reasons within individuals may be calculated.

1. Claim to not be killed [5 units]

2. Claim to not be allowed to die [4 units]

3. Claim that another is not killed [3 units]

4. Claim that another is not allowed to die [2 units]

Using these values, we can reexamine the Empathetic Woollard Trolley’s two outcomes:

Sticking to the Individualistic Restriction, we must examine the most harmed individuals in either outcome to make a decision rather than aggregating. As the DDA suggests, B as an individual experiences less harm when allowed to perish than C experiences when killed.

As the numbers change, however, such as in the Empathetic Thomson Trolley, we find that the accumulation of empathetic claims eventually overtakes the significance of the DDA:

            Empathetic Thomson Trolley:

As previously stated, the only difference between Woollard Trolley and Thomson Trolley (whether both are in their original or empathetic forms) cases are the numbers. With the realistic consideration made for the presence of empathetic claims (with marginally egotistic weights, mind you) the appropriate response considering the Individualistic Restriction has switched in favor of the individuals on the main track. This approach, with minimal additional psychological claims considered, very quickly reinforces the intuitive responses to either case.

I will now address the egoism/altruism assumption made when I assigned the relative weights to the psychological claims. Assigning weights that favor altruism presents no problem for my argument, for increasing the relative weights of these claims will only decrease the number of additional individuals on the main track needed to metaphorically tip the scale against the DDA. At extremely high levels of altruism, this point could come before the numbers change at all. However, assuming such extreme levels of altruism is in itself counter-intuitive (with intuitive values likely being at or near neutral). When considering high levels of egoism (thus, lower weights to the altruistic claims), the argument still holds true. In cases of similar numbers (like Woollard Trolley variations), the DDA will take precedence. In cases of greater number disparity, Extreme Trolley still holds that, so long as individuals still hold some concern for others (however tiny!) the accumulation of empathetic claims will eventually overtake the DDA. The case of total egoism (0 weight to altruism) is total narcissism and only reinforces this argument (as an absolute narcissist will, of course, always put their needs above any number of others’ needs). In any case, extreme altruism and egoism certainly do not appear to be intuitive assumptions of humanity. Marginal or neutral claims, such as my own of marginal egoism, seem far more realistic. In fact, the mathematical outcomes of any equal inputs of altruism/neutrality/egoism fall directly in line with what we see in reality: Egoists/Narcissists will disregard the numbers, intuitive individuals will likely abandon the DDA after any or marginal changes in the numbers, and total altruists will provide selfless responses in any situation.

In this paper, I explained Woollard’s argument for the existence of a New Problem of Numbers in Morality and her subsequent conclusion regarding Strong Nonconsequentialism: That the Strong Nonconsequentialist must either reject intuitive responses to the trolley cases or reject the Individualistic Restriction. I then argued against this conclusion by highlighting the underlying issues of Woollard’s provided trolley cases and providing an alternative Strong Nonconsequentialist solution that takes these issues into account. By way of considering additional psychological claims (specifically empathy), the Strong Nonconsequentialist may hold the intuitive response to either trolley case so long as they are commonsensical themselves. Therefore, Woollard’s conclusion regarding Strong Nonconsequentialism is false.

Jackson Anderson is a junior at the University of Florida, where he will graduate with a BS in Finance and begin the MSF program. Jackson has an interest in the social sciences and philosophy, which he hopes will provide him the perspective needed to be a strong leader and promoter of change in the modern business world.

[1] “…the justifiability of a moral principle depends only on various individuals’ reasons for objecting to that principle or alternatives to it” (Scanlon, 1998, p. 229)

[2] Woollard spends much of her article, The New Problem of Numbers in Morality (2014), explaining how F. M. Kamm’s Balancing/Tiebreaker Argument (1985) and Véronique Munoz-Dardé’s Non-Comprehensive Reasons Argument (2005) both seem to be unable to be extended to a more complex problem of numbers.

[3] It is important to note an additional, minor alternative for the Strong Nonconsequentialist: Rejecting the intuitive response to Woollard Trolley (DDA) in order to accept the intuitive response to Thomson Trolley and avoid the Extreme Trolley dilemma. This response is blatantly concerning for the Strong Nonconsequentialist, as this inherently accepts the significance of numbers and rejects the Individualistic Restriction. This point is made without this alternative being explicitly written about (As it is an underlying feature of the overall dilemma), which is why I did not initially include it. Note also that rejecting both intuitive responses still leaves the Strong Nonconsequentialist with the extreme implications of Extreme Trolley.

[4] One may object to this method by claiming that either egotistic (1 & 2) or altruistic (3 & 4) claims are “infinitely” superior to the other and, thus, cannot be compared directly with finite values. However, this claim would result in extreme implications highlighted by Extreme Trolley by forcing proponents to either ignore the DDA or ignore the numbers (each having counter-intuitive results).

References 

Kamm, F. M. (1985). Equal treatment and equal chances. Philosophy & Public Affairs, 14(2), 177-194. https://www.jstor.org/stable/2265456

Munoz-Dardé, V. (2005). The distribution of numbers and the comprehensiveness of reasons. Proceedings of the Aristotelian Society New Series, 105, 191-217. https://www.jstor.org/stable/4545435

Scanlon, T. M. (1998). What we owe to each other. Harvard University Press.

Taurek, J. M. (1977). Should the numbers count? Philosophy & Public Affairs, 6(4), 293–316. https://www.jstor.org/stable/2264945

Thomson, J. J. (1985). The trolley problem. The Yale Law Journal, 94(6), 1395–1415. https://digitalcommons.law.yale.edu/ylj/vol94/iss6/5

Woollard, F. (2014). The new problem of numbers in morality. Ethical Theory and Moral Practice, 17, 631-641. https://doi.org/10.1007/s10677-014-9496-x